18.S096: Max-Cut and Approximation Algorithms

The eight set of Lecture notes, now about Max Cut and Approximation Algorithms, is available here. They include five open problems, briefly documented here. Please see the notes for a lot more detail on the problems, relevant references and more.

Open Problem 8.1. (Unique Games Conjecture)

Is the Unique Games conjecture true? In particular, can it be refuted by a constant degree Sum-of-squares relaxation?

Open Problem 8.2. (Sum of Squares approximation ratio for Max-Cut)

What is the approximation ratio (or integrality gap) for the Sum-of-Squares (SOS) relaxation of degree 4 for the Max-Cut problem? What about other constant degrees?

Open Problem 8.3. (The Grothendieck Constant)

What is the value of the (real) Grothendieck constant?

Open Problem 8.4. (The Paley Clique Problem)

What is the clique number of the Paley graph? Can the the SOS degree 4 analogue of the theta number help upper bound it?

Open Problem 8.5. (Maximum and minimum bisections on random regular graphs)

Given a $d$ -regular graph on $n$ nodes $G$ . Let $MaxBis(G)$ and $MinBis(G)$ denote, respectively, the size of its largest and smallest bisection. Is it true that for every $d$

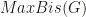
$MaxBis(G)$ $+ MinBis(G)$ $=$ $\frac{d}{2} + o(1)$ ,

where $o(1)$ is a term that goes to zero as $n$ grows?